中学受験理科の「ばねとグラフ」では、ばねの伸びや力の関係をグラフで表し、交点を利用して問題を解くことがよくあります。グラフの交点は、ばねの力のバランスや共通の値を見つける重要なポイントです。本記事では、ばねの性質とグラフの読み取り方、交点を使った問題の解き方をわかりやすく解説。受験対策に役立つコツも紹介しています。
「ばねの長さとグラフ」基本問題
Q:下のグラフは、つるしたおもりの重さとばねA、Bの長さとの関係を表したものである。図のように、ばねAとBを並列につなぎ、ばねにとり付けた棒の中央におもりをつるした。このとき、ばねAとBは同じ長さになり、棒は水平になっていた。これについて、以下の各問いに答えよ。
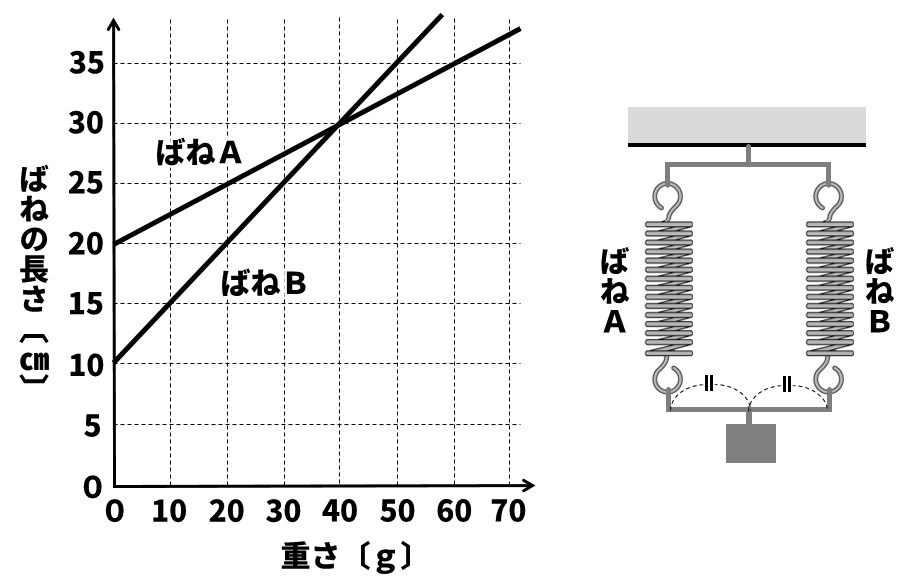
(1)図のようにおもりをつるしたとき、ばねAの長さは何cmになっているか。
(2)つるしたおもりは何gか。
ばねの長さのグラフの交点
ばねの長さとおもりの重さの関係を表すグラフは、次のように読み取ります。
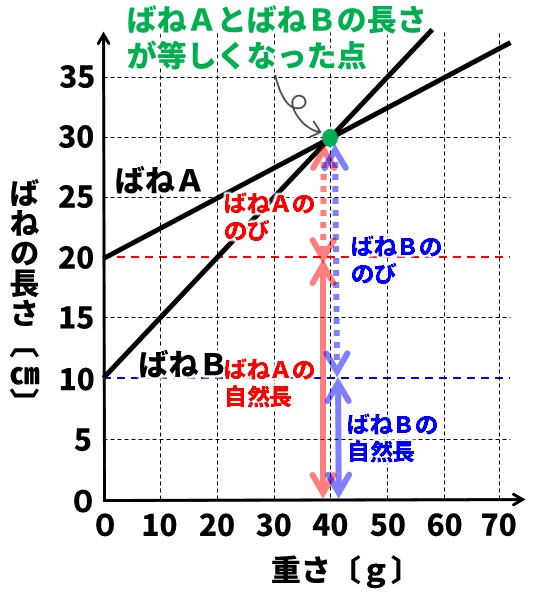
上の緑で表された点は、同じ重さのおもりがつるされたとき、ばねの長さが同じになったことを表しています。ここが今回の問題のポイントです。
それでは、今回の問題の答え合わせを行いましょう。
「ばねの長さとグラフ」基本問題 解答
グラフを確認し、ばねの長さが同じになっている点を探します。そのばねの長さが、ばねAとばねBの長さになり、そのときのおもりの重さがばねA、Bそれぞれに加わっている重さになります。
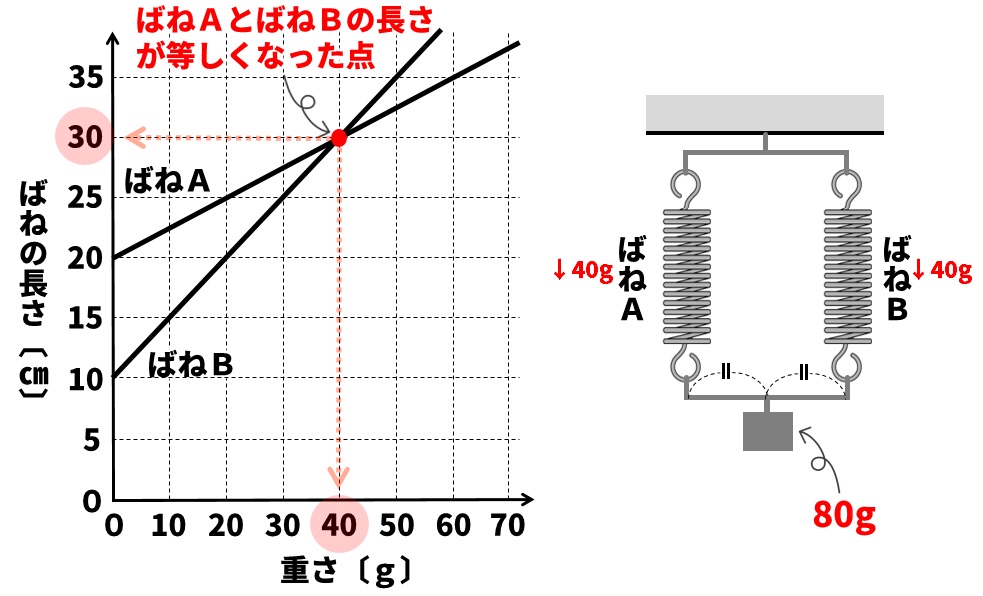
このときのばねの長さは、A、Bともに30cmになります。つるされているおもりの重さは、並列につながれているので40g✕2=80gになります。
A (1)30cm (2)80g
コメント