てこのつり合いの応用問題です。太さが違う重さがあるてこの問題に挑戦します。
「太さがあるてこ」応用問題
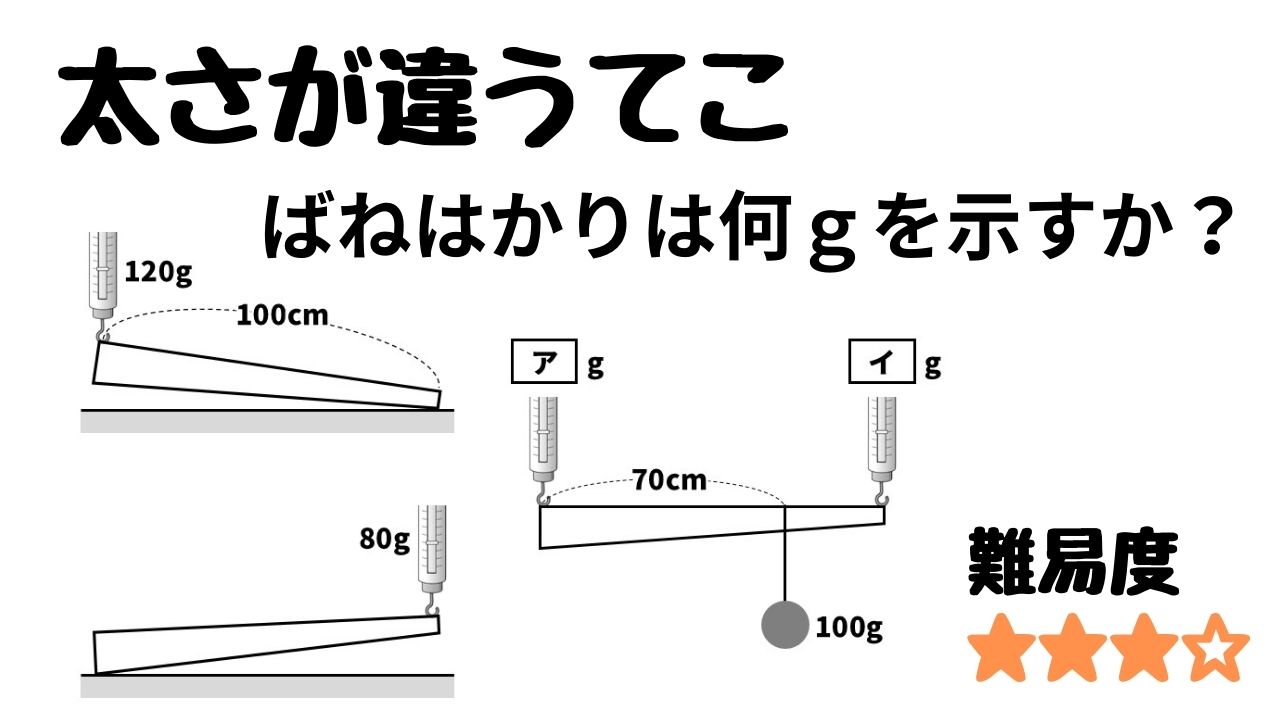
Q:下の図のような、長さ100cmの棒の両はしを、ばねばかりで支えると、それぞれ120gと80gを示した。この棒の両はしをばねはかりでつるし、棒の左はしから70cmのところに、100gのおもりをつるした。これについて、以下の各問いに答えよ。
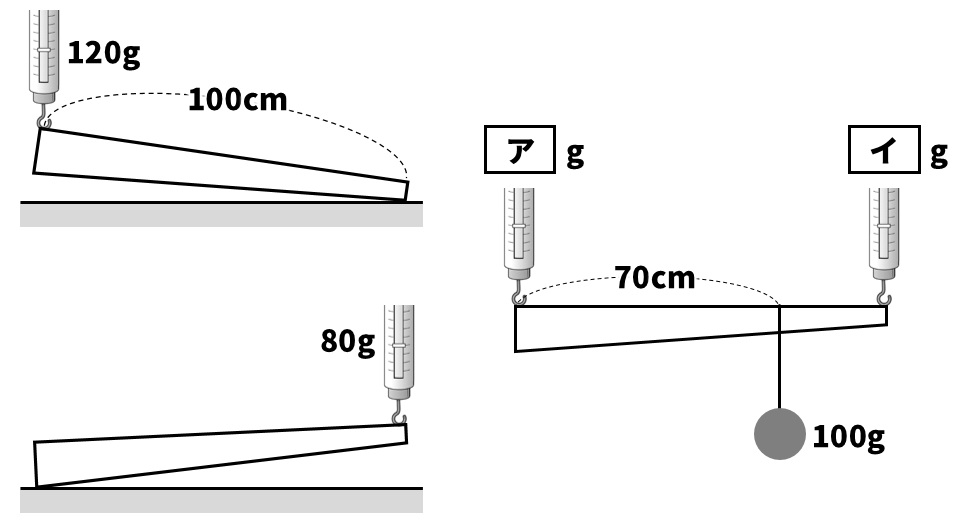
(1)この棒の重さは何gか。
(2)( ア )、( イ )はそれぞれ何gを示すか。
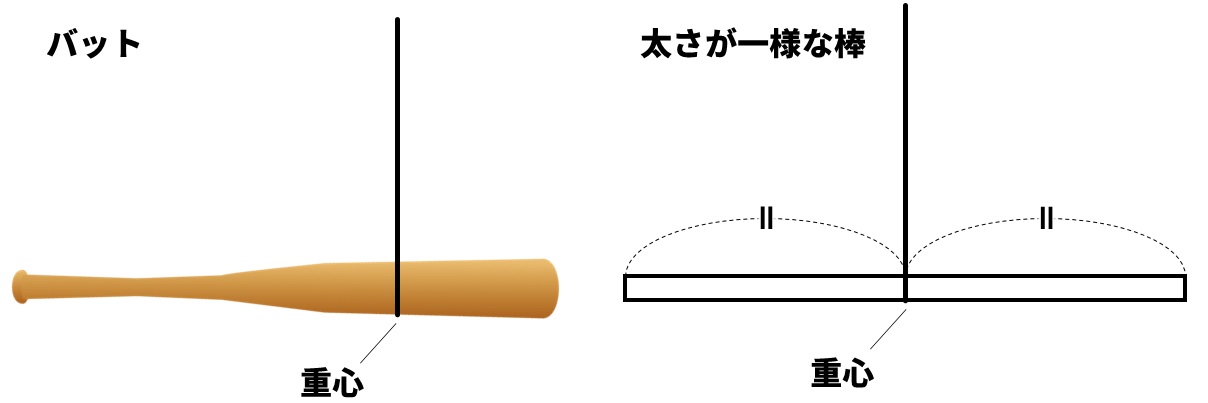
太さが違うてこの重心
太さが違うてこの問題を解く場合は、まず重心を考えます。重心とはものの重さのかかる点のことで、重心にひもをつけてつるすと棒が水平になるところになります。太さが一様な棒の場合は、重心は棒の中央になりますが、太さが違う場合は重心は中央になりません。
太さが違う棒の場合、両はしの重さの逆比から重心の位置を求めます。今回の問題の場合、左はしをつるすと120g、右はしをつるすと80gを示していることから、重さの比は、120:80=3:2になります。3:2の逆比が重心の位置になるので、重心のいちは棒の長さを2:3に分けたところになります。
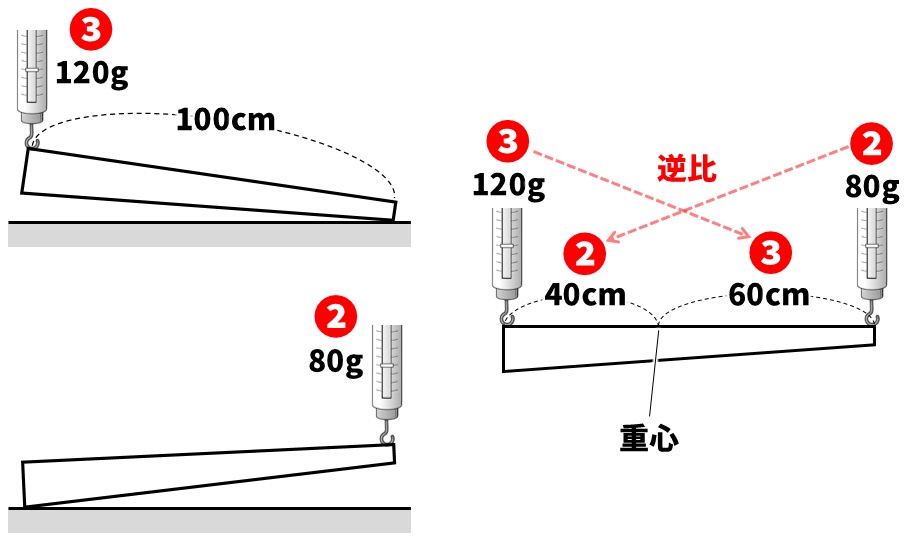
重心の位置がわかったら、そこに棒の重さをつるします。左はしが120g、右はしが80gを示しているので、この棒の重さは、120+80=200gになります。
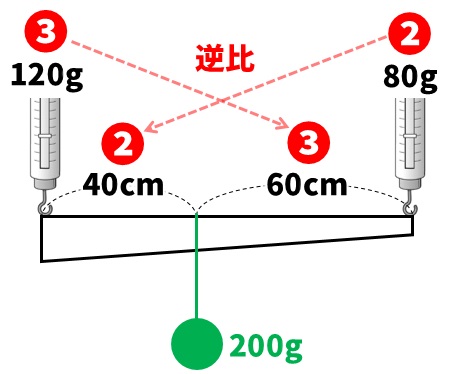
このように、重心の位置を求めて、そこに棒の重さをつるすせば、あとはいつも通りてこのつり合いを計算していくだけになります。
支点の位置を設定してこのつり合いを考える
重心に棒の重さをつるした後ですが、この問題は支点の位置が示されていません。このような場合は、勝手にイメージしやすい場所を支点にしましょう。今回は、左はしを支点に設定します。右はしを支点にしてももちろん解けます。
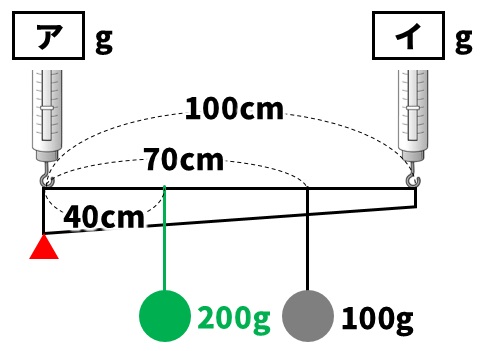
左はしを支点として、左に回転させるはたらきと右に回転させるはたらきが等しくなることを利用してばねはかりの値を求めます。
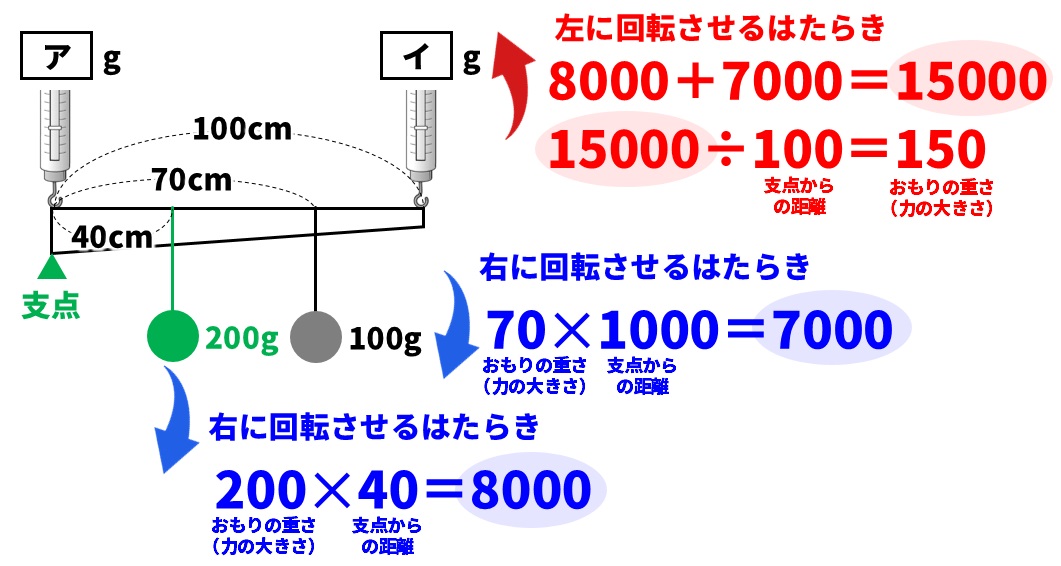
これで( イ )が何gなのかがわかります。
力のつり合いを考える
最後に( ア )が何gを示すのかを求めます。棒にはたらく力のつり合いがわかれば簡単に出せます。
棒を下向きに引く力は、200+100=300gになります。上向きに引く力は150gなので、( ア )は、300ー150=150gになります。
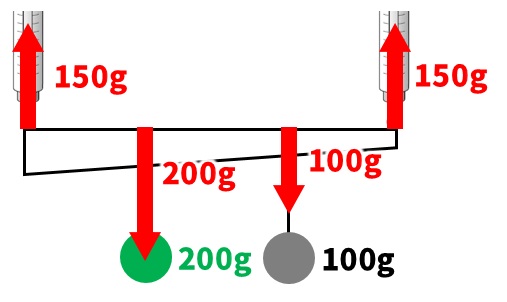
「太さがあるてこ」応用問題 解答
解答の前に、解き方をまとめると次のようになります。
- 棒の両はしの重さの逆比から、重心の位置を求める。
- 重心に棒の重さをつるす。
- 支点の位置を決める。
- 右と左に回転させるはたらきをそれぞれ求める。
- 力のつり合いを求める。
以上のようにすれば、てこの応用問題も解けるようになります。
A
(1)200g
棒の両はしの重さを足します。120+80=200g
(2)ア:150g イ:150g
コメント