中学受験理科「ばねののびと比」比を使って解く問題

ばねののびの比を使って解く問題に挑戦します。グラフからばねののびの比を求め、その比を使って計算できるようになりましょう。

「ばねののびと比」応用問題

Ｑ：下のグラフは、つるしたおもりの重さとばねＡ、Ｂの長さとの関係を表したものである。図のように、ばねＡとＢを直列につなぎ、ばねＡとばねＢの合計の長さが90cmになるようして固定した。これについて、以下の各問いに答えよ。

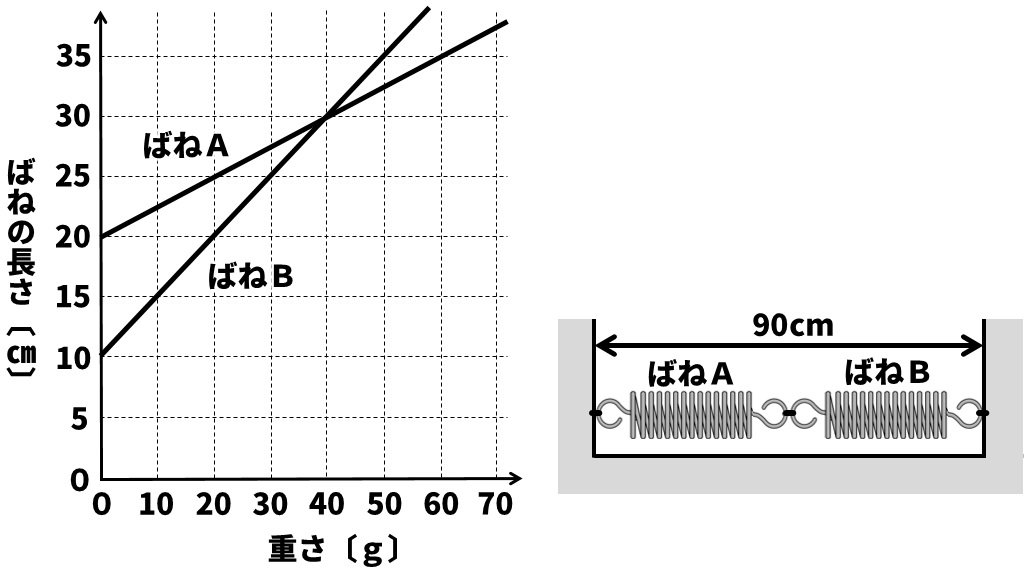
（1）図のときの、ばねAとばねBののびの合計は何cmか。

（2）ばねＡとばねＢの長さは、それぞれ何cmか。

【問題DL】ばねののびと比

ばねののびの比を使って解く方法

ばねののびの比がわかれば、比を使ってばねの長さを計算することができます。今回の問題で練習しましょう。まずは、グラフや表から何ｇで何cmのびるばねなのかを確認します。次の❶から❸の手順で考えます。

❶同じ重さのおもりをつるしたときののびの比を求める

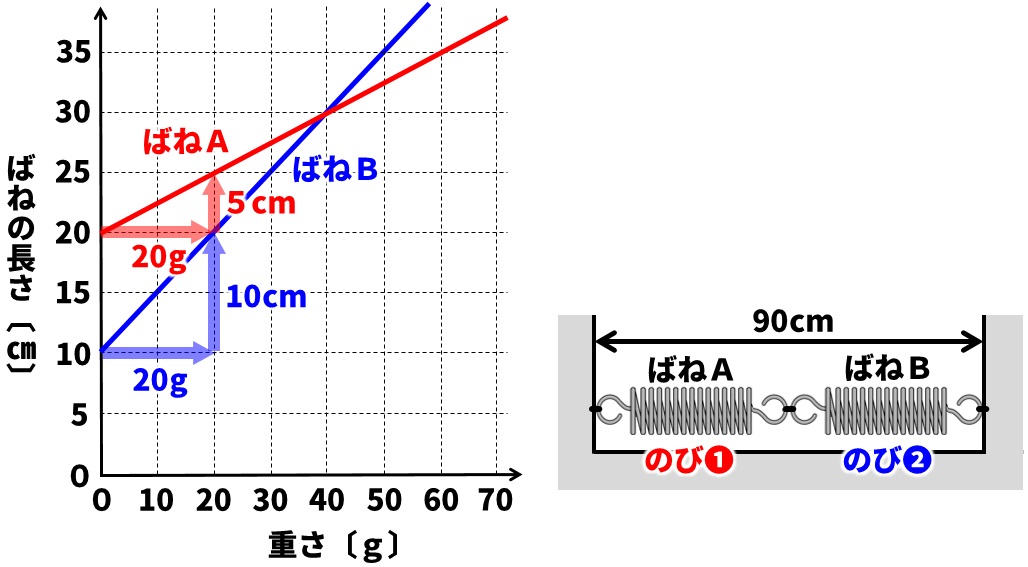
グラフより、ばねＡは20ｇで5cmのびるばねであると確認できます。ばねＢは20ｇで10cmのびるばねであると確認できます。したがって、同じ重さのおもりをつるしたときのばねののびの比は、
ばねＡ：ばねＢ＝➀：➁
であることがわかります。

❷自然長を引いてばねののびの合計を求める

グラフより、ばねＡの自然長（何もつるしていないときのばねの長さ）が20cm、ばねＢの自然長が10cmだとわかるので、
90cmー（20cm＋10cm）＝60cm
ばねＡとばねＢののびの合計は、60cmであるとわかります。

❸ばねののびの合計を、比を使ってそれぞれののびにする

ばねののびの合計が60cmで、ばねＡ、Ｂののびの比が➀：➁だとわかったので、比を使って60cmを➀：➁に分けます。比の合計は、
➀＋➁＝③なので、
60÷③＝20
ばねＡののびは、
20✕➀＝20cm
ばねＢののびは、
20✕➁＝40cm
自然長を足して、それぞれのばねの長さに直します。
ばねＡの長さは、
20cm＋20cm＝40cm
ばねＢの長さは、
10cm＋40cm＝50cm
となります。

このように、ばねの比を求めて、ばねののびの合計を比を使って分ける解き方になります。

「ばねののびと比」応用問題　解答

Ａ　（1）60cm（2）ばねＡ：40cm　ばねＢ：50cm

答えを出した後も、40＋50＝90になるなど、確かめ算をするように心がけましょう。