中学受験算数「多角形の面積を求める問題」です。
多角形の面積を求める問題
次の図の斜辺部分の面積を求めなさい。
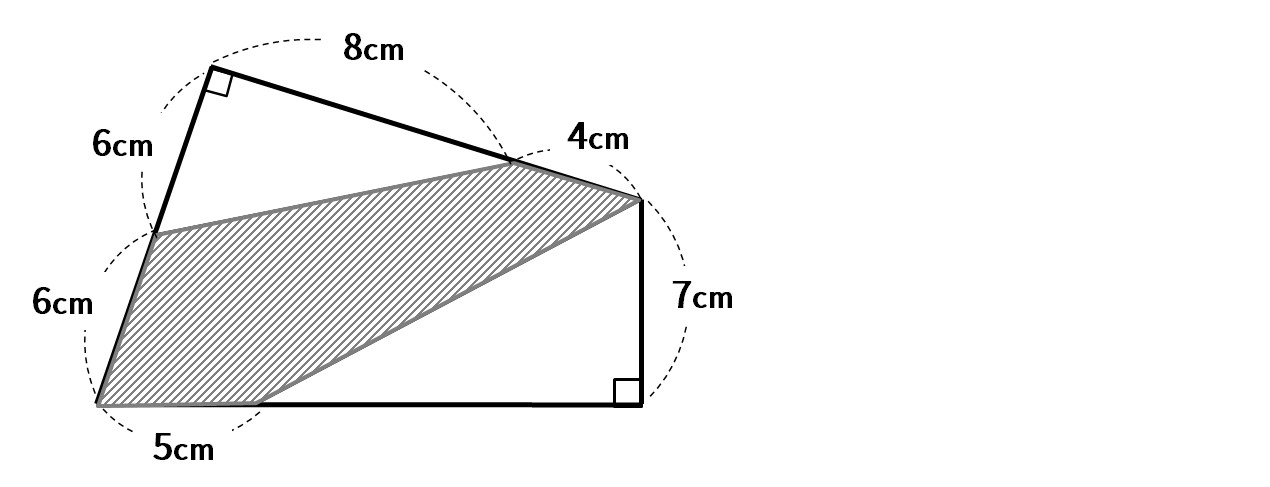
多角形の面積を求める問題の解き方
多角形の面積の求め方は、多角形を対角線で三角形に分けて、それぞれの三角形の面積を加える。
図の中の垂直な2本の直線が、三角形の底辺と高さになるように分ける。
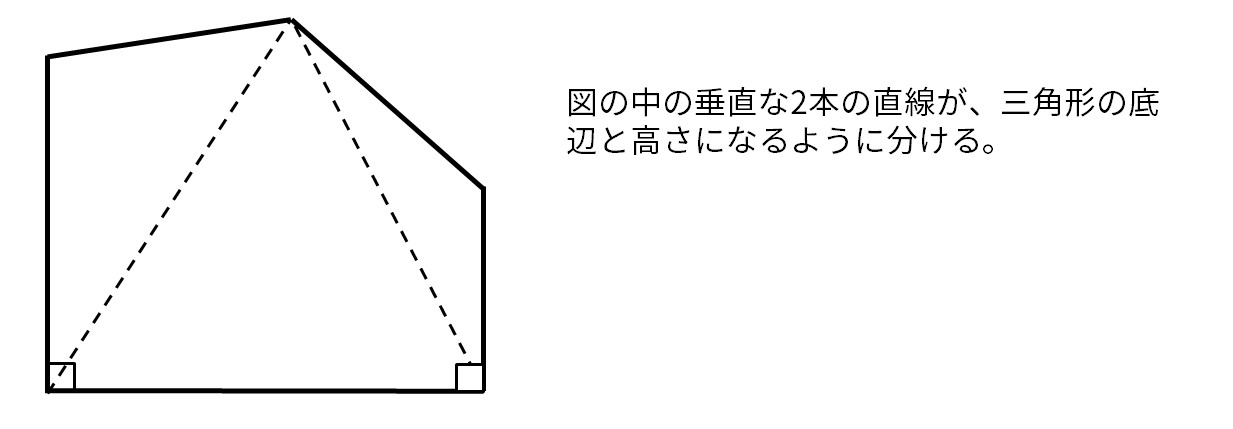
多角形の面積を求める問題の解説
斜線部分の面積を直接求めることはできないので、補助線をひき、3つの三角形㋐㋑㋒に分けて考える。
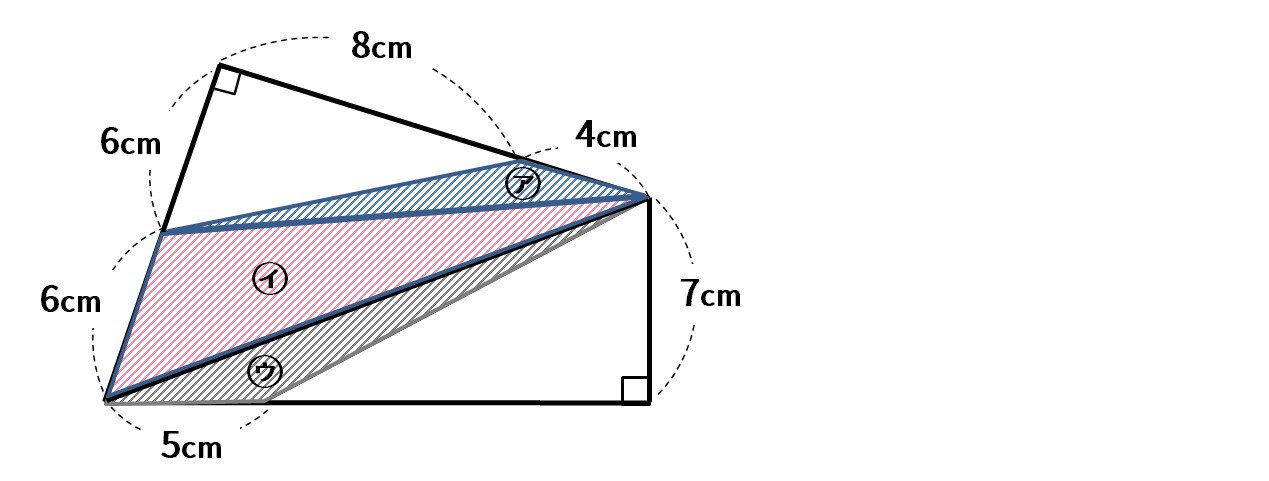
㋐…4×6÷2=12
㋑…6×(8+4)÷2=36
㋒…5×7÷2=17.5
したがって、斜線部分の面積は、
12+36+17.5=65.5
多角形の面積を求める問題の解答
65.5cm2
このような複合図形の面積の求め方は、まずは、今回のように補助線を引いて考えるのが、最初の手順です。補助線を引いてひけないとき、他の方法(➊全体からまわりを引く。➋図形をひとつにまとめる。➌等積変形➍比)を考えます。
多くの中学受験でも出題されるので、確実に正解していきましょう。
コメント