中学受験算数「中心角が異なるおうぎ形の面積比の問題」です。今回は、中心角が異なるおうぎ形の問題です。中心角が等しい場合との区別をしっかりして解いていきましょう。
中心角が異なるおうぎ形の面積比の問題
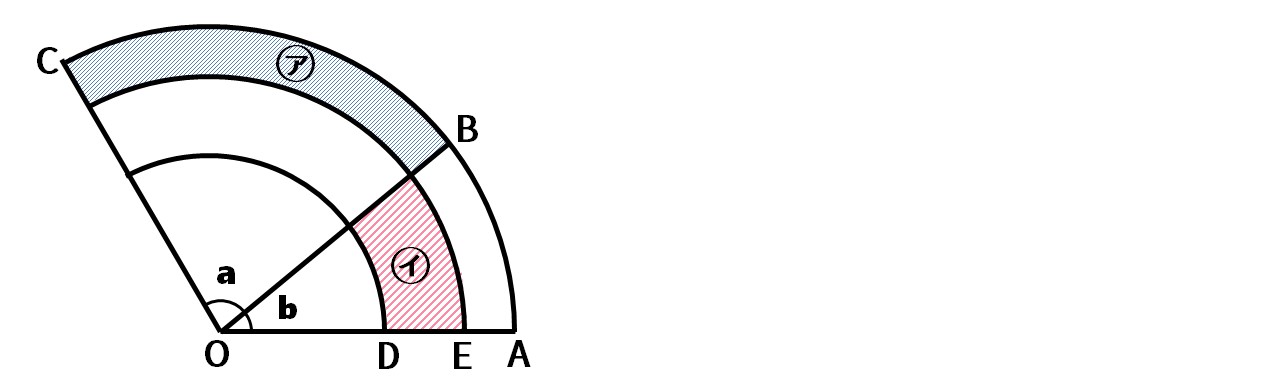
次の図のおうぎ形で、角aの大きさは角bの大きさの2倍、ODとEAの長さは等しく、DEの長さはODの長さの2倍です。このとき、㋐の部分と㋑の部分の面積の比を求めなさい。
中心角が異なるおうぎ形の面積比のポイント
中心角が異なるおうぎ形の面積比は、
半径の比×半径の比×中心角の比
で求める。
中心角が異なるおうぎ形の面積比の問題の解説
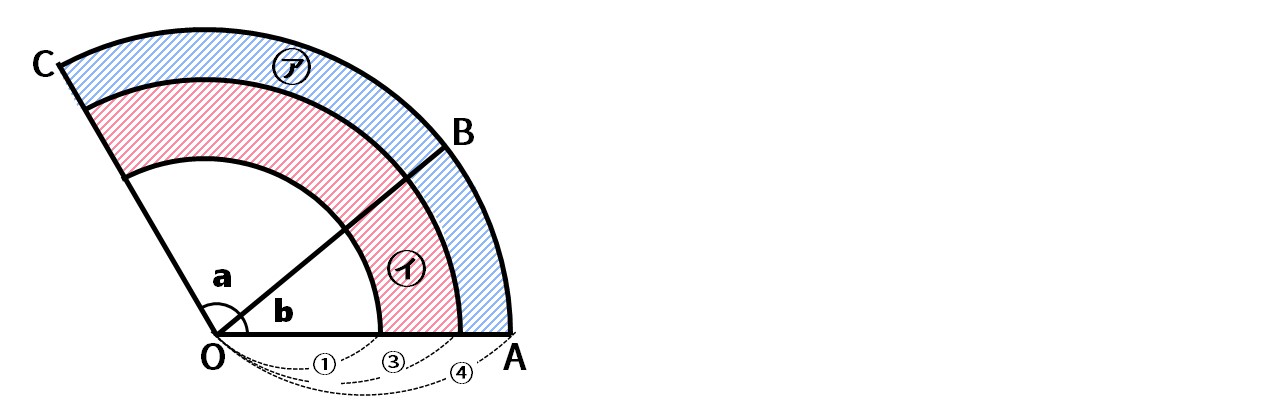
<手順➊>
3つのおうぎ形の半径の比は、
1:(1+2):(1+2+1)
=1:3:4
<手順➋>
㋐と㋑の部分の面積の比は、
{(4×4-3×3)×2}:{(3×3-1×1)×1}
=7:4
中心角が異なるおうぎ形の面積比の問題の解答
7:4
おうぎ形の基本公式(➊おうぎ形の面積、➋おうぎ形の弧の長さ、➌おうぎ形の中心角)をおさえて、様々なパターンの問題をこなして本番に臨もう。
コメント