中学受験算数「切断された円柱・角柱の体積の問題」です。切断されたときの円柱・角柱の性質を知っておきましょう。
切断された円柱・角柱の体積の問題
次の図の立体の体積を求めよ。ただし、円周率は、3.14とします。
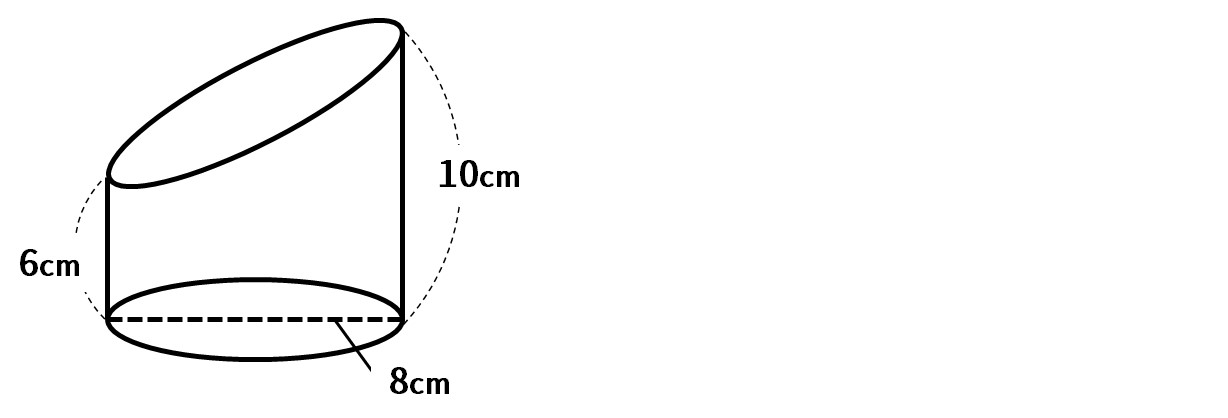
切断された円柱・角柱の体積のポイント
斜めに切った円柱・角柱の体積は、
同じ形の立体2つ分の体積÷2
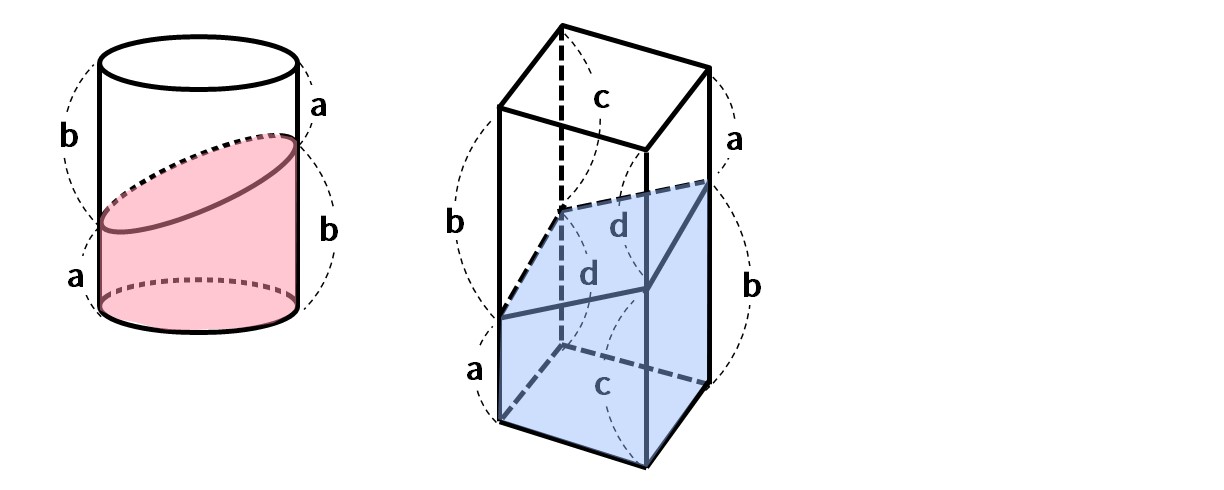
同じ形なので、2つ組み合わせて、円柱・角柱を作る。
切断された円柱・角柱の体積の問題の解説
<手順1>
(ポイント)の図のように、同じ形の立体を2つ合わせて円柱をつくると底面の半径は、8÷2=4
<手順2>
4×4×3.14×(10+6)÷2
=401.92cm2
円柱の体積=底面積×高さ
この円柱の高さは、10+6=16cmとなります。
この円柱の高さは、10+6=16cmとなります。
切断された円柱・角柱の体積の問題の解答
401.92cm2
今回のように切断された立体の体積を求めさせる問題は、ときどき出題されるので、今回の解き方も押させておくといいでしょう。

コメント