複数のてこが組み合わさったモビールの解き方を学習します。基本的なてこのつり合いがわかっていれば必ずとける問題です。
「モビール」応用問題
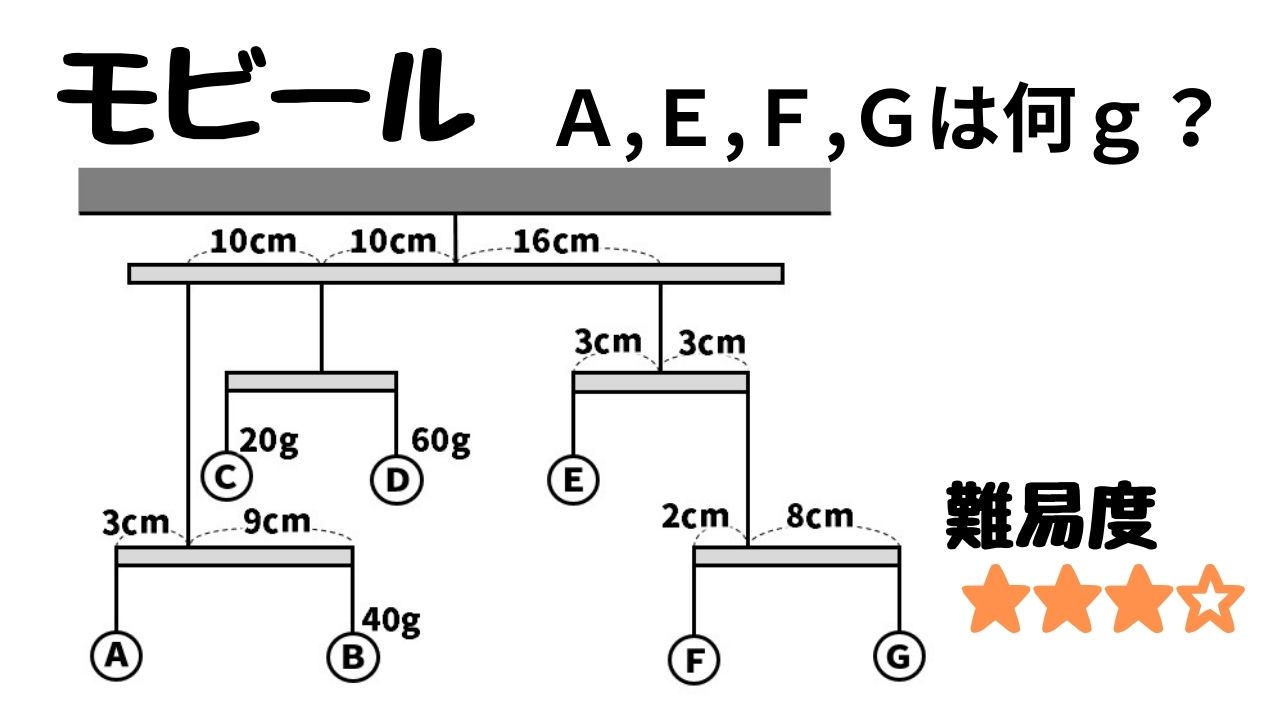
Q:下の図は、おもりと棒がつり合っている状態を表したものである。これについて、以下の各問いに答えよ。ただし、棒とひもの重さは考えなくてよいものとする。
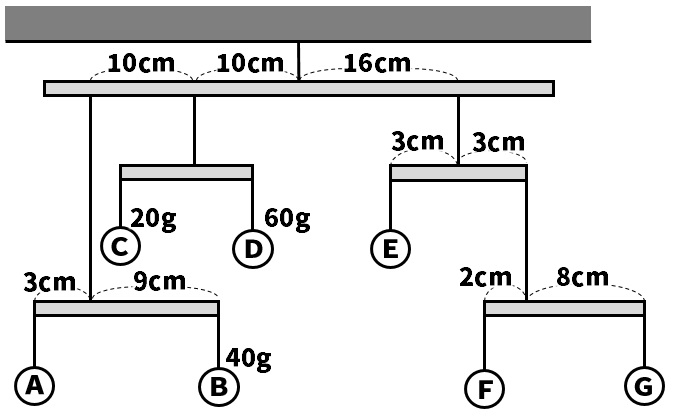
(1)おもりAは何gか。
(2)おもりEは何gか。
(3)おもりBを50gに変えたとき、おもりと棒がつり合った状態にするには、Fを何gにする必要があるか。
モビールとは
モビールとは、複数の棒(てこ)と糸をつなげ天井からぶら下げたものです。したのようなオブジェになります。
一か所のおもりを変えると、全体のバランスをとるために他のおもりも変えないといけなくなります。今回は、モビールの問題に挑戦しましょう。
モビールの解き方
モビールを解くとき、基本的に下につるされているてこのつり合いから考えていきますが、わかるところのてこのつり合いをどんどん解いていくという感じで大丈夫です。このとき、
- 左右の支点からの距離✕おもりの重さが等しくなる
- 支点からの距離の比とおもりの重さの比が逆比になる
の両方を使って考えていきます。とりあえず、今回の問題で考えていきましょう。
「モビール」応用問題 (1)(2)解答
まずは、左側の下の方の棒のつり合いから考えていきます。支点からの距離の比は、
3cm:9cm=❶:❸なので、おもりの重さは❸:❶になります。
Bの40gが❶の重さなので、Aの重さは、
40g✕❸=120gだとわかります。
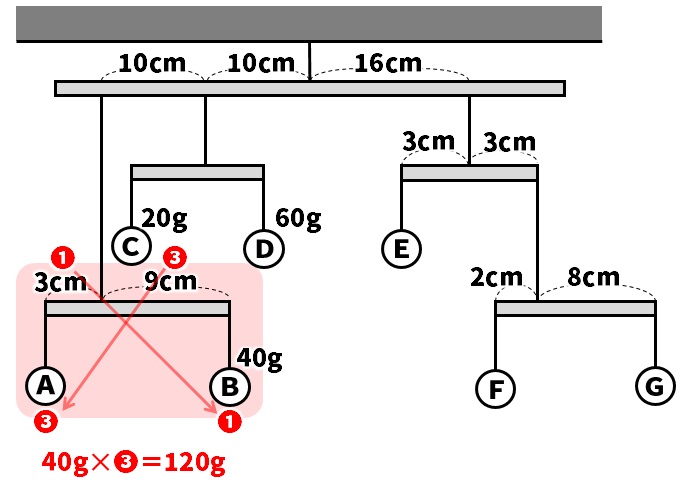
次は、全体のつり合いを考えます。一番上にある長い棒のつり合いです。
おもりAとBが棒を左に回転させようとするはたらきは、
(120g+40g)✕(10cm+10cm)=3200
おもりCとDが棒を左に回転させようとするはたらきは、
(20g+60g)✕10cm=800
合計すると、3200+800=4000になります。
棒を右に回転させようとするはたらきも4000になります。
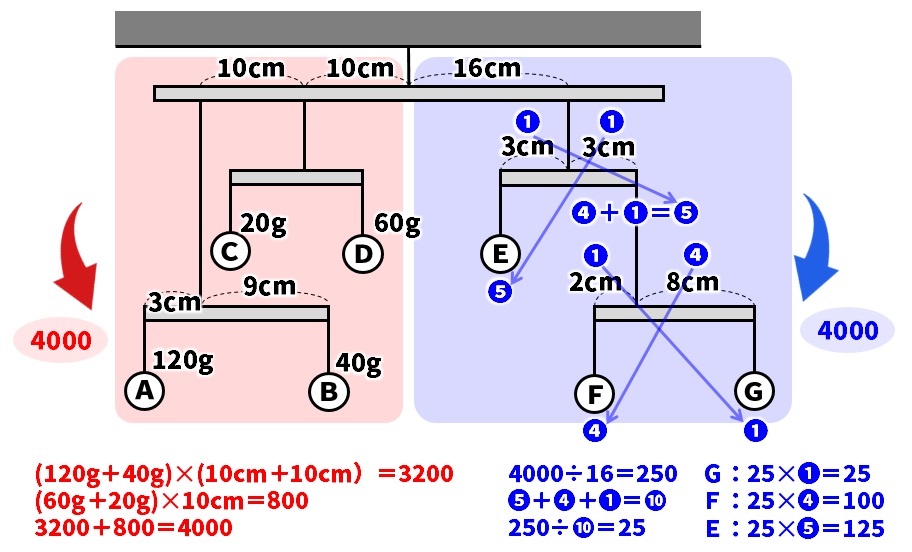
次は、右側の回転させるはたらき4000を使ってE~Gの重さを考えていきますが、比を使って考え行きましょう。
おもりFとGのつり合いですが、支点からの距離の比は、
2cm:8cm=❶:❹なので、おもりの比は❹:❶になります。
次は、おもりEのつり合いを考えます。支点からの距離の比は、
3cm:3cm=❶:❶なので、おもりの比も❶:❶になります。
ここではFとGのおもりの比の合計が❹+❶=❺なので、おもりEとF+Gのおもりの比は、❺:❺に比を合わせておきましょう。
E、F、Gのおもりの比の合計は、
❹+❶+❺=➓になるので、❶あたりの重さは、
4000÷16cm=250g
250g÷➓=25になります。
おもりEの重さは、25✕❺=125g
おもりFの重さは、25✕❹=100g
おもりGの重さは、25✕❶=25gとなります。
A (1)120g (2)125g
「モビール」応用問題 (3)解答
おもりBが50gに変わってしまったので、もう一度最初から棒のつり合いを同じ手順で考え直します。
左側の下の方の棒のつり合いからです。支点からの距離の比は、
3cm:9cm=❶:❸なので、おもりの重さは❸:❶になります。
Bの50gが❶の重さなので、Aの重さは、
50g✕❸=150gだとわかります。
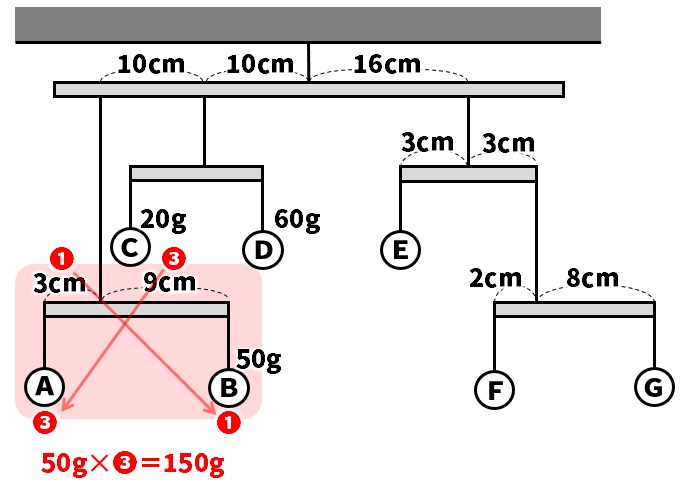
次は、全体のつり合いを考えます。一番上にある長い棒のつり合いです。
おもりAとBが棒を左に回転させようとするはたらきは、
(150g+50g)✕(10cm+10cm)=4000
おもりCとDが棒を左に回転させようとするはたらきは、
(20g+60g)✕10cm=800
合計すると、4000+800=4800になります。
棒を右に回転させようとするはたらきも4800になります。
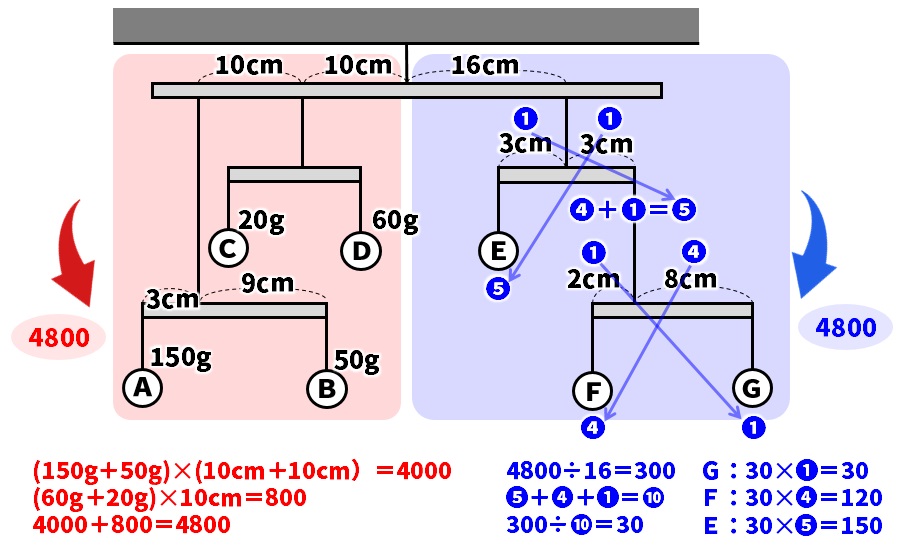
右側の回転させるはたらき4800を使ってE~Gの重さを考えます。どの棒も支点から距離は変わっていないので、上で計算したおもりの比を使います。
比の合計は、❹+❶+❺=➓になるので、❶あたりの重さは、
4800÷16cm=300g
300g÷➓=30になります。
おもりEの重さは、30✕❺=150g
おもりFの重さは、30✕❹=120g
おもりGの重さは、30✕❶=30gとなります。
A (3)120g
コメント