中学受験の図形問題では、「おうぎ形」に関する出題が頻繁にあり、中でも「中心角が等しいおうぎ形の面積比」はよく出る応用テーマです。実は、中心角が同じ場合、面積比は“半径の2乗の比”になるというルールがあり、これを理解して使いこなせるかが得点のカギになります。この記事では、公式の成り立ちから考え方、典型的な問題パターンまで、図を使ってわかりやすく解説。苦手な人もスッキリ理解できます!
中心角が等しいおうぎ形の面積比の問題
次の図は、中心角120°のおうぎ形です。A:Bの面積の比をできるだけ小さな整数の比で答えなさい。円周率は3とします。
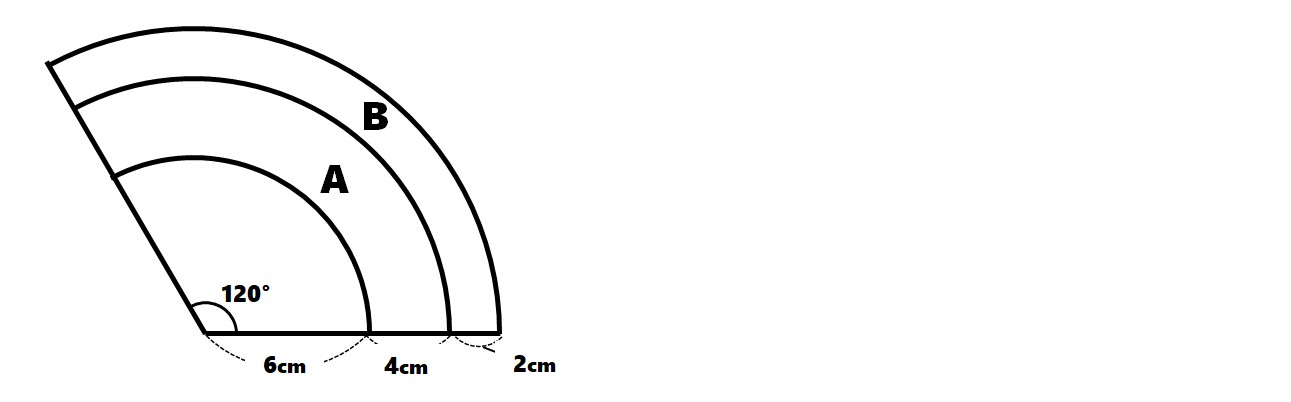
中心角が等しいおうぎ形の面積比のポイント
中心角の等しいおうぎ形の面積比は、
●半径の比×半径の比
となる。
中心角が等しいおうぎ形の面積比の問題の解説
※円周率は使わなくても解ける!
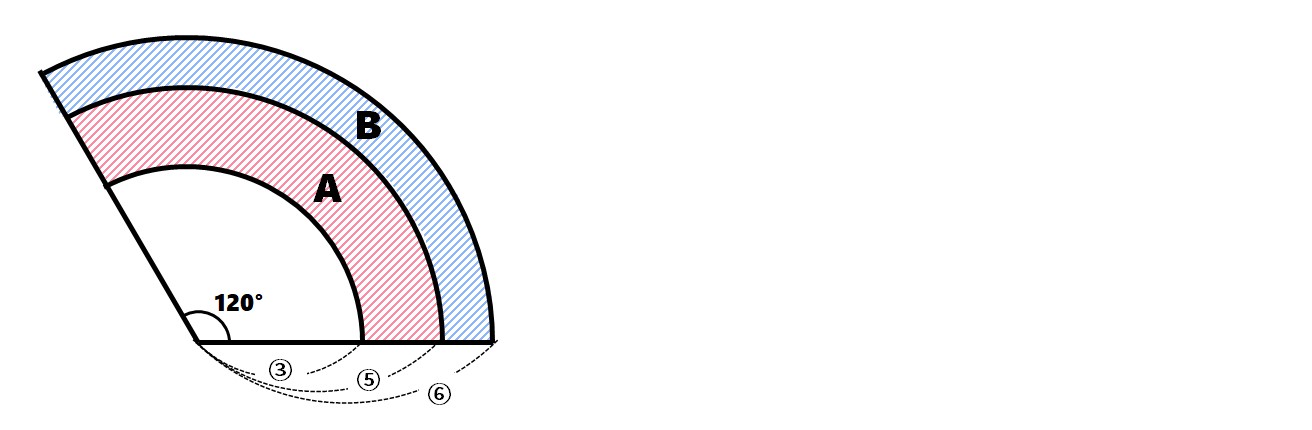
<手順1>
3つのおうぎ形の半径の比は、
6:(6+4):(6+4+2)
=3:5:6
<手順2>
AとBの面積比は
(5×5-3×3):(6×6-5×5)
=16:11
中心角が等しいおうぎ形の面積比の問題の解答
16:11
今回の問題のように、その求め方を知っていれば、普通に解くよりはやく答えを導けるだけでなく、計算ミスも減ります。いろいろな解き方をマスターしていきましょう。
コメント