中学受験算数「等積変形を利用した問題」です。
等積変形を利用した問題
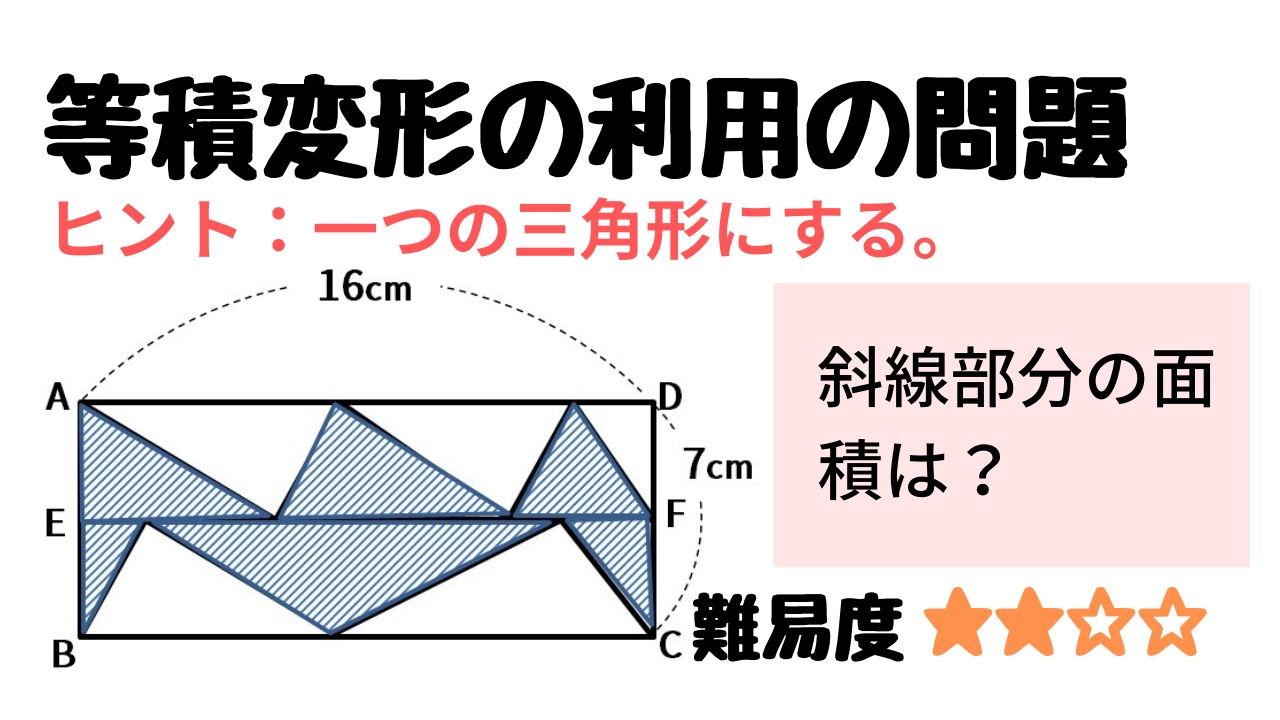
次の図の四角形ABCDは長方形で、それぞれ辺AB,辺CDのまん中の点です。斜線部分の面積を求めなさい。
.jpg)
等積変形のポイント
等積変形の利用:高さの等しい三角形の面積の和
⇢等積変形で1つの三角形にする
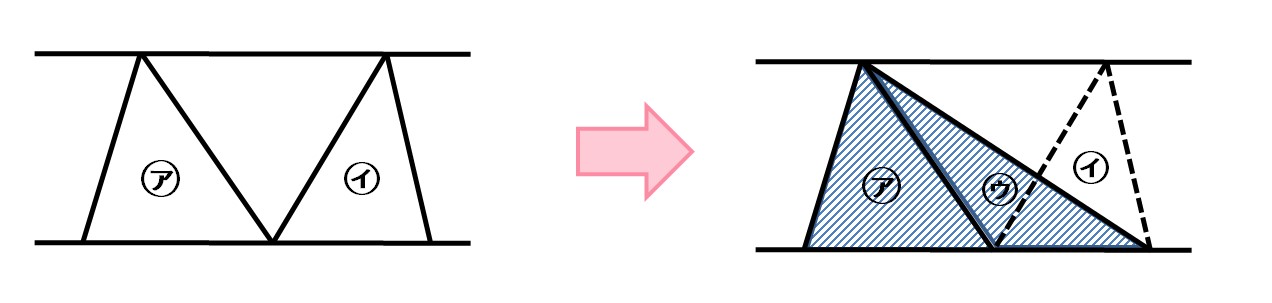
次の図で、㋑の面積=㋒の面積であるから、㋐の面積+㋑の面積=㋐㋒の三角形の面積として求められます。
等積変形を利用した問題のポイント
次の図で、等積変形により、ピンクの三角形の2つの和(三角形AEF+三角形BEF)となります。
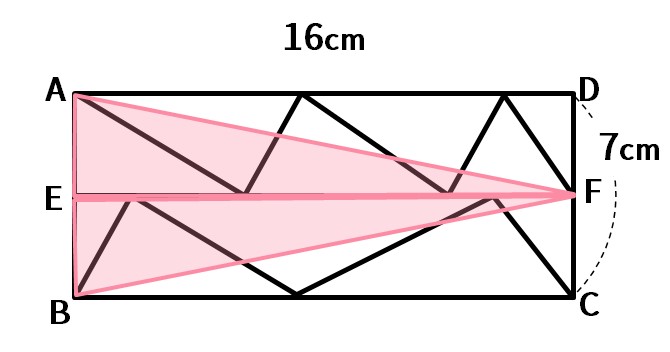
つまり、三角形ABEの面積を求めることになるので、
7×16÷2=56
等積変形を利用した問題の解答
56cm2
コメント