中学受験算数「角すい上の最短距離の問題」です。
角すい上の最短距離の問題
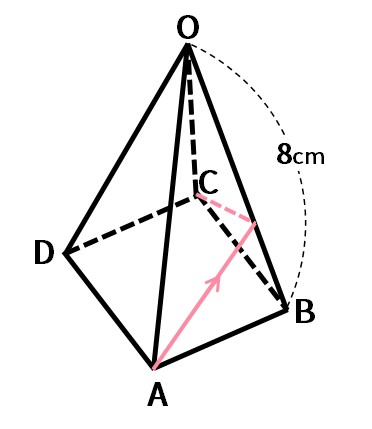
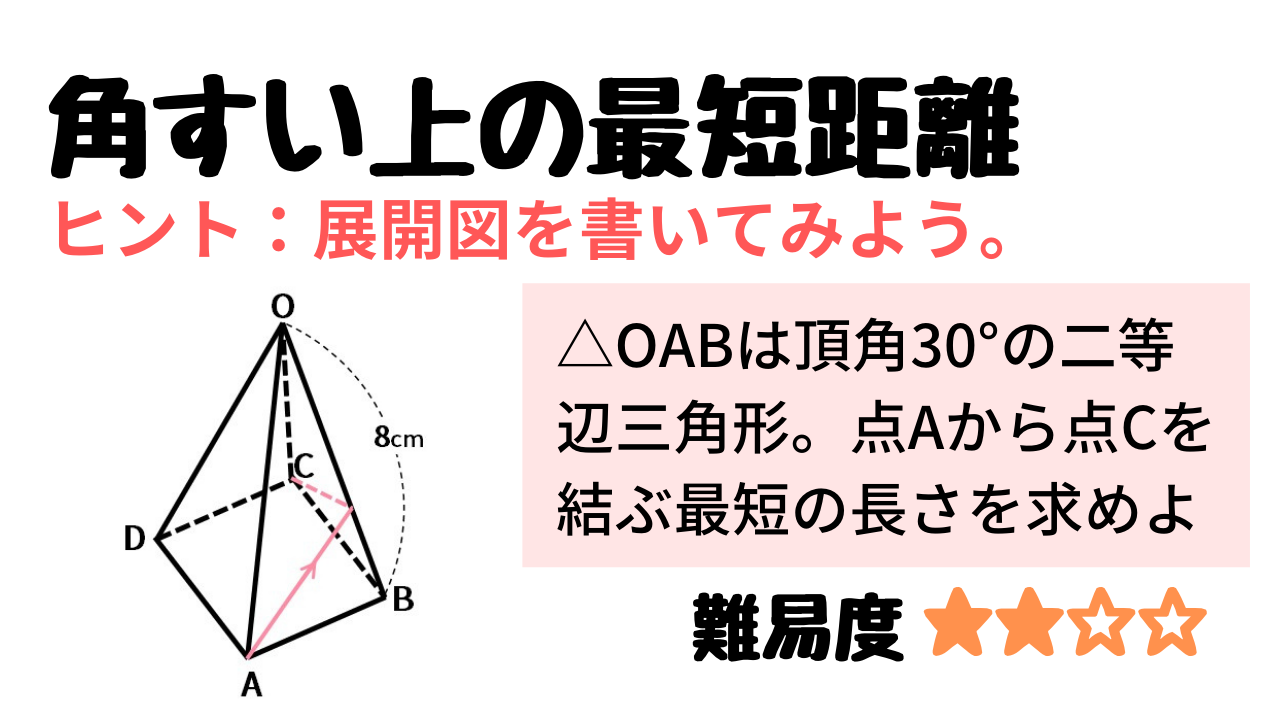
図のような、正四角すいO-ABCDがあります。この正四角すいの側面の三角形OABはOA=OB=8cm、角AOB=30°の二等辺三角形で、底面は正方形です。このとき、点Aから側面を通り点Cに行く最短の道のりを求めなさい。
角すい上の最短距離のポイント
■角すい上の最短距離
側面や底面の展開図で最短距離にしたい2点を直線で結ぶ。
※角すいの展開図は何通りもありますが、題意(問題文)に沿って、関係するところの展開図を書きましょう。
角すい上の最短距離の問題の解説
<手順➊>
ACが連続した直線になるように展開図をかく。
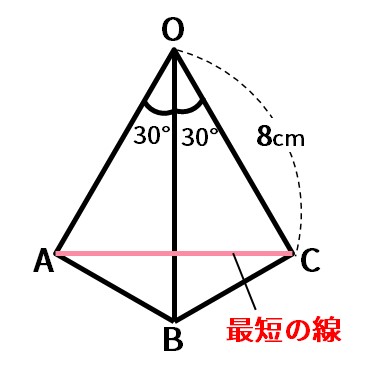
<手順➋>
角AOC=60°だから、三角形OACは正三角形である。
よって8cm
角すい上の最短距離の問題の解答
8cm
コメント