中学受験理科の「ばね」分野で差がつくのが、直列つなぎ・並列つなぎに関する応用問題です。基本の比例関係をしっかり理解していても、つなぎ方が変わると急に難しく感じる受験生も多い分野。本記事では、ばねの直列・並列つなぎの考え方を復習しながら、よく出る応用パターンや計算問題の解き方のコツを図付きでわかりやすく解説します。入試で差をつけたい人は必見です!
「ばねの直列・並列つなぎ」応用問題
Q:下の表は、硬さが異なる2つのばねA、Bについての、ばねののびとつるしたおもりの重さとの関係を表したものである。次の(1)、(2)のようにばねをつなぐと、全体のばねののびは何cmになるか。ただし、ばね自体の重さは考えないものとする。

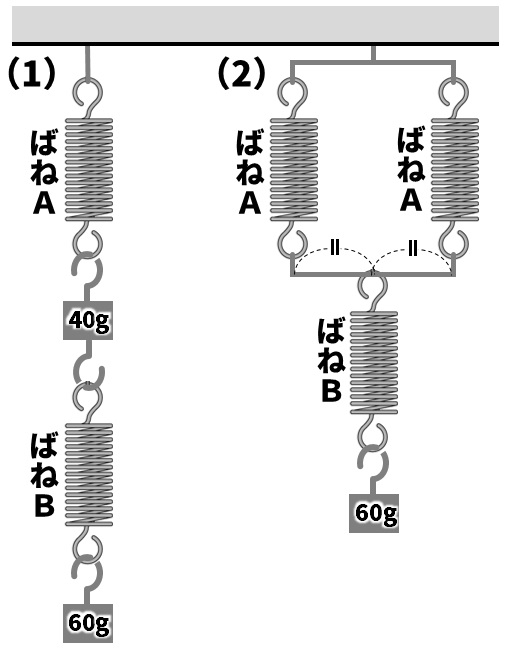
ばねののびと重さの比例関係を使ってのびを計算すること、直列つなぎと並列つなぎののびの関係を使ってのびを計算することの2点が問われています。
「ばねの直列・並列つなぎ」応用問題 (1)の解答
(1)の問題は、ばねが直列につながれている問題です。ばねAとばねBの間におもりがつるされていることに注意が必要です。このようにつながれている場合、上にあるばねAには合計100gの重さがかかり、下にあるばねBには60gの重さがかかります。
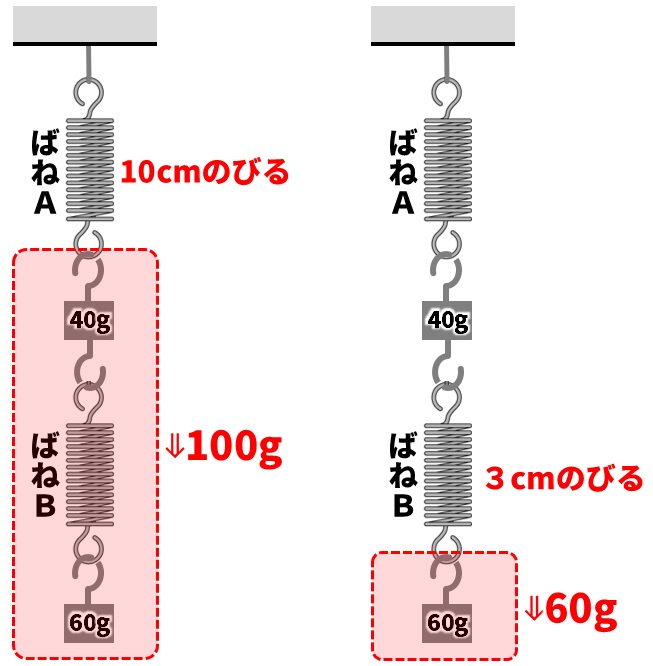
表より、ばねAは20gで2cmのびるばねだとわかるので、
20:2=100:□
□=10
10cmのびるとわかります。
表より、ばねBは20gで1cmのびるばねだとわかるので、
20:1=60:□
□=3
3cmのびるとわかります。
全体のばねののびは、
10+3=13
A:13cm
「ばねの直列・並列つなぎ」応用問題 (2)の解答
(2)の問題は、ばねが並列につながれていて、その下にさらにばねがある問題です。ばねが並列につながれている場合は、下の図のように重さが2つに分けられます。
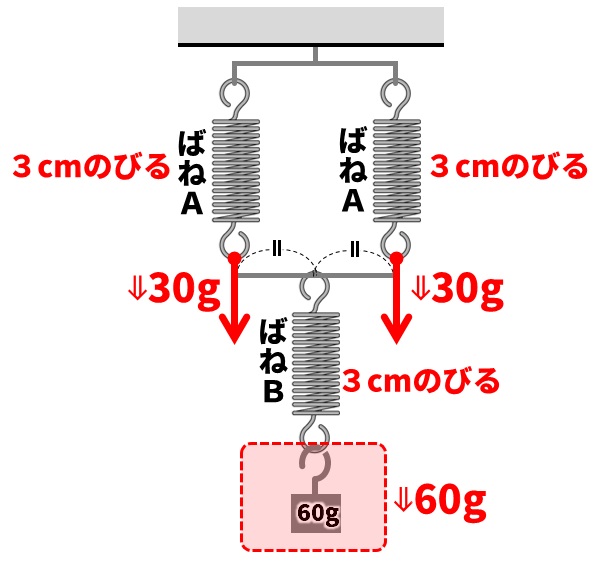
下にあるばねBには60gの重さがかかり、上にあるばねAには、それぞれ60gの半分の30gの重さがかかります。
表より、ばねAは20gで2cmのびるばねだとわかるので、
20:2=30:□
□=3
それぞれ3cmのびるとわかります。
表より、ばねBは20gで1cmのびるばねだとわかるので、
20:1=60:□
□=3
3cmのびるとわかります。
全体のばねののびは、
3+3=6
A:6cm
このように、ばねの下に何gのおもりがつるされているかをしっかり確認しながら解いていくことが重要です。

コメント