中学受験理科「太さが一様で重さがあるてこ」重心に棒の重さをつるす

てこに重さがある場合の解き方を学習します。まずはてこの太さが一様なパターンです。

「太さが一様で重さがあるてこ」基本問題

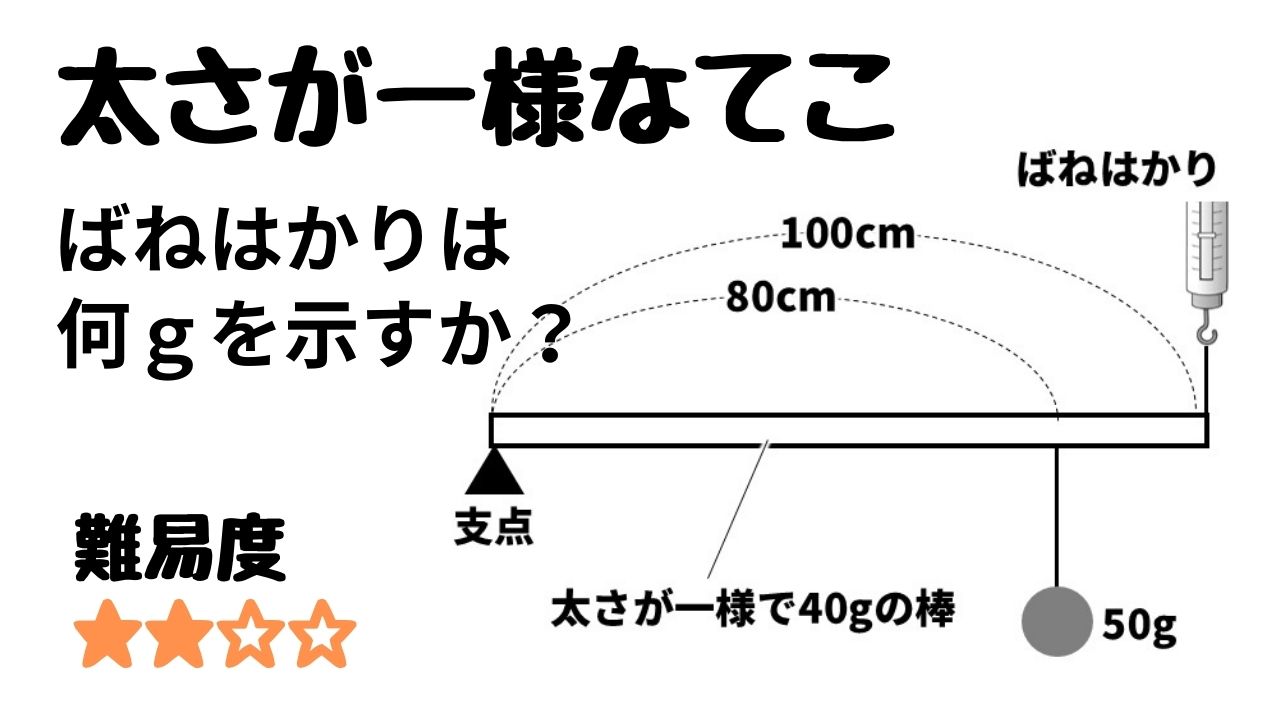
Ｑ：下の図のような長さ100cm棒のはしを支点で支え、50gのおもりを支点から80cm離れた位置につるし、もう一方のはしをばねはかりで支えた。これについて、次の各問いに答えよ。ただし、棒の重さは40ｇで太さは一様であるものとする。

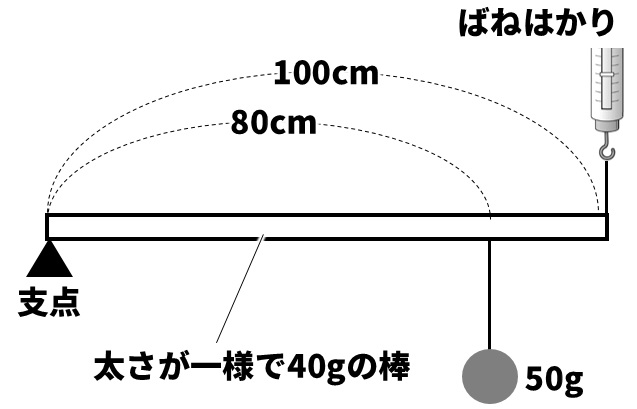
（1）図のとき、ばねはかりは何ｇを示すか。

（2）図のとき、支点には何ｇの重さがかかっているか。

てこに重さがある場合は、重心に棒と同じ重さのおもりをつるしていると考えて解きます。重心とは、ものの重さのかかる点のことで、下の図のように重心にひもをつけてつるすと、物体を支えることができます。

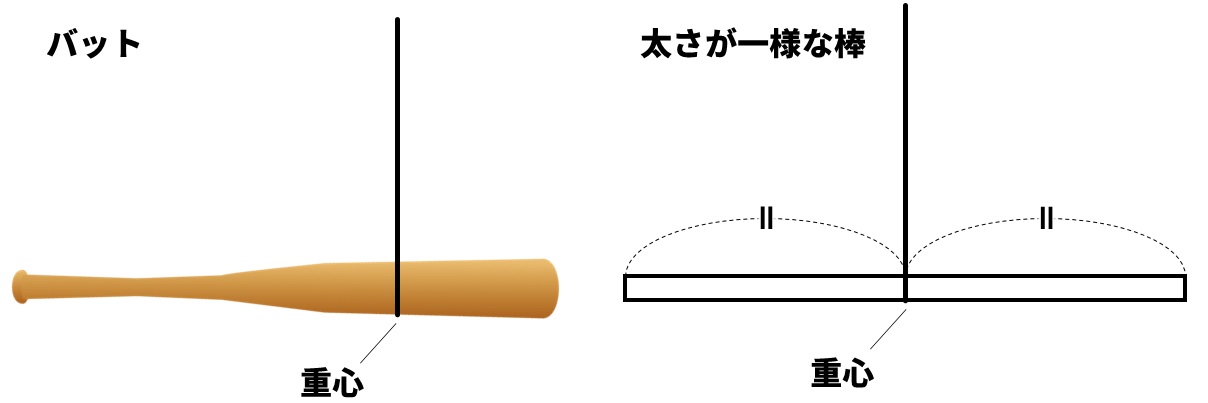
太さが一様な棒の場合、重心はちょうど真ん中に位置します。太さが一様な重さがある棒の問題の場合、中心の重心に棒の重さをつるして問題を解きます。

この問題では棒の太さが一様なので、重心に棒の重さと同じ重さをつるして考えます。こうすることで棒の重さを考えなくて済むようになります。

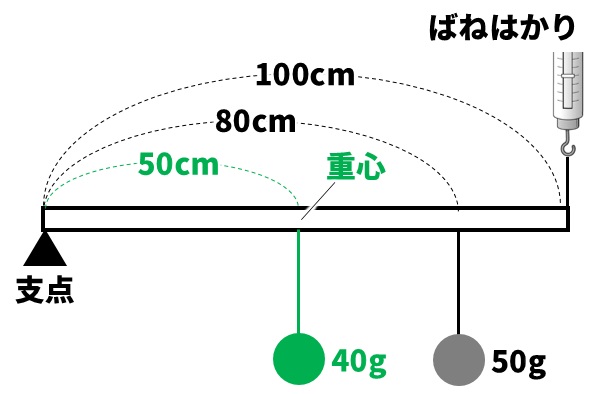
長さが100cmの棒なので、その中心である支点から50cmの位置に、棒の重さである40ｇのおもりをつるします。あとは、てこのつり合いを計算していくだけです。

支点を中心に、棒を右に回転させるはたらきと左に回転させるはたらきが等しくなるように、ばねばかりが示す重さを求めていきます。

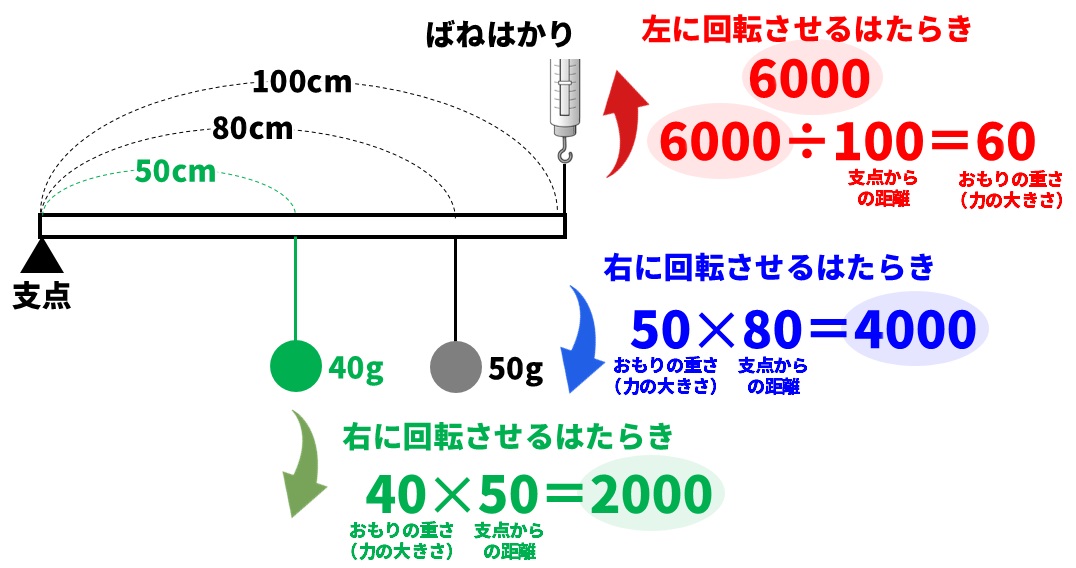
棒を右に回転させるはたらきは、棒のおもさと50ｇのおもりの合計になります。
50gのおもり…　50g✕80cm＝4000
40gの棒…　40g✕50cm＝2000
棒を右に回転させるはたらきの合計は、4000＋2000＝6000

棒を左に回転させるはたらきも6000になるので、ばねはかりが示す値は、
6000÷100cm＝60g

支点にかかる重さは、上向きのおもさと下向きのおもさが同じになることから求めます。下向きの力は、棒の重さと重りの重さの合計になります。
40g＋50g＝90g
上向きの力は、ばねはかりの値と支点で支える力の合計になります。したがって。支点で支える力は、
90g－60g＝30gとなります。

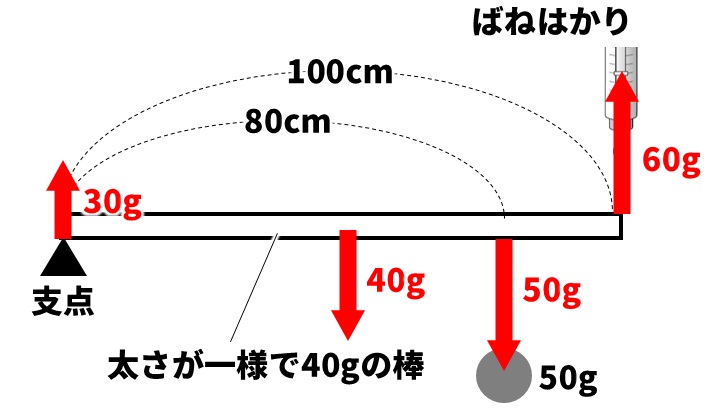
Ａ（1）60ｇ　（2）30ｇ